komposisi fungsi

Pengertian Fungsi Komposisi

Fungsi komposisi yaitu penggabungan operasi pada dua jenis fungsi f (x) dang (x) hingga menghasilkan fungsi baru. Operasi fungsi komposisi biasa yaitu dilambangkan dengan “o” dan dibaca dengan komposisi atau bundaran.

Fungsi baru yang bisa terbentuk dari f (x) dan g (x) yaitu:
(f o g)(x) = g dimasukkan ke f
(g o f)(x) = f dimasukkan ke g

Fungsi tunggal itu merupakan fungsi yang bisa dilambangkan dengan huruf “f o g” ataupun juga bisa dibaca dengan “fungsi f bundaran g”. Fungsi “f o g” ialah fungsi g yang dikerjakan terlebih dahulu lalu dilanjutkan dengan f. Sedangkan, untuk fungsi “g o f” dibaca dengan fungsi g bundaran f. Maka, “g o f” ialah fungsi dengan f dikerjakan terlebih dahulu daripada g.

Rumus Fungsi Komposisi

fungsi komposisi

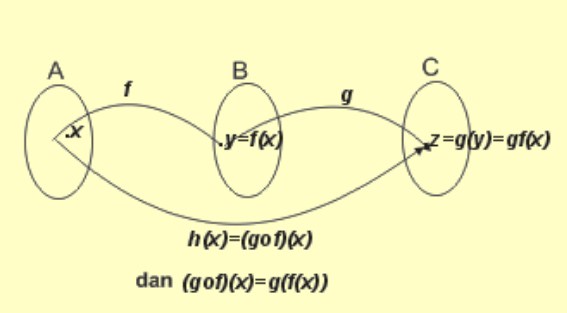
Dari rumus tersebut, definisi yang di dapat ialah :

Jika f : A → B ditentukan rumus y = f (x)
Jika g : B → C ditentukan rumus y = g (x)

Jadi, hasil fungsi g dan f :

h (x) = (g o f)(x) = g( f(x))
Dari penjelasan tersebut bisa disimpulkan bahwa fungsi yang melibatkan fungsi f dan g bisa ditulis :
(g o f)(x) = g (f(x))
(f o g)(x) = f (g(x))

Contoh Soal

Contoh Soal 1

Diberikan dua buah fungsi yang masing-masing f (x) dan g (x) berturut-turut yaitu :
f (x) = 3x + 2
g (x) = 2 − x

Tentukanlah:
a) (f o g) (x)
b) (g o f) (x)

Jawaban
Data:
f (x) = 3x + 2
g (x) = 2 − x

a) (f o g)(x)

“Masukkanlah g (x) nya kef (x)”

hingga menjadi:
(f o g)(x) = f ( g(x) )
= f (2 − x)
= 3 (2 − x) + 2
= 6 − 3x + 2
= − 3x + 8

b) (g o f ) (x)

“Masukkanlah f (x) nya ke g (x)”

Hingga menjadi :
(f o g) (x) = g (f (x) )
= g ( 3x + 2)
= 2 − ( 3x + 2)
= 2 − 3x − 2
= − 3x

Contoh Soal 2

Diketahui fungsi f (x) = 3x − 1 dan g (x) = 2×2 + 3. Nilai dari komposisi fungsi ( g o f )(1) =….?
A. 12
B. 8
C. 7
D. 11
E. 9

Jawaban
Diketahui:
f (x) = 3x − 1 dan g (x) = 2×2 + 3
( g o f )(1) =…?

Masukkanlah f (x) nya pada g (x) lalu isi dengan 1
(g o f) (x) = 2 (3 x − 1) 2 + 3
(g o f) (x) = 2 (9 x 2 − 6x + 1) + 3
(g o f) (x) = 18x 2 − 12x + 2 + 3
(g o f) (x) = 18×2 − 12x + 5
(g o f) (1) = 18 (1) 2 − 12(1) + 5 = 11

Contoh Soal 3

Diberi dua buah fungsi:
f (x) = 2x − 3
g (x) = x2 + 2x + 3

Jika (f o g)(a) adalah 33, tentukanlah nilai dari 5a

Jawaban:
Cari terlebih dahulu (f o g)(x)
(f o g)(x) sama dengan 2(x2 + 2x + 3) − 3
(f o g)(x) sama dengan 2×2 4x + 6 − 3
(f o g)(x) sama dengan 2×2 4x + 3

33 sama dengan 2a2 4a + 3
2a2 4a − 30 sama dengan 0
a2 + 2a − 15 sama dengan 0

Faktorkan:
(a + 5)(a − 3) sama dengan 0
a = − 5 ataupun a sama dengan 3
Hingga
5a = 5(−5) = −25 atau 5a = 5(3) = 15

Contoh Soal 4

Jika (f o g)(x) = x² + 3x + 4 dan g(x) = 4x – 5. Berapakah nilai dari f(3)?

Jawaban:
(f o g)(x) sama dengan x² + 3x + 4
f (g(x)) sama dengan x² + 3x + 4
g(x) sama dengan 3 Jadi,
4x – 5 sama dengan 3
4x sama dengan 8
x sama dengan 2
f (g(x)) = x² + 3x + 4 dan untuk g(x) sama dengan 3 didapat x sama dengan 2
Hingga : f (3) = 2² + 3 . 2 + 4 = 4 + 6 + 4 = 14

Demikianlah penjelasan dari Rumusrumus.com tentang fungsi komposisi, Semoga bermanfaat