persamaan linear tiga variabel

Sistem Persamaan Linear Tiga Variabel (SPLTV)

Sistem persamaan linear tiga variabel adalah sistem persamaan yang terdiri dari tiga persamaan dimana masing-masing persamaan memiliki tiga variabel. Contoh SPLTV dengan variabel 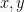 dan :

dimana 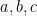 dan 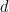 adalah bilangan-bilangan real.

Pada SPLTV terdapat 2 cara penyelesaian, yaitu:

1. Metode Subtitusi

Langkah yang dilakukan pada metode ini yaitu:

1. Ubah salah satu persamaan yang ada pada sistem dan nyatakan  sebagai fungsi dari  dan , atau  sebagai fungsi dari  dan , atau  sebagai fungsi dari  dan ..
2. Subtitusikan fungsi  atau  atau  dari langkah pertama pada dua persamaan yang lain, sehingga diperoleh SPLDV.
3. Selesaikan SPLDV yang diperoleh dengan metode yang dibahas pada penyelesaian SPLDV di atas.

Contoh Soal:
Tentukan penyelesaian dari sistem persamaan linear tiga variabel berikut:

.

Mau latihan soal? Yuk jawab pertanyaan di Forum StudioBelajar.com

Jawab:

Langkah pertama, nyatakan persamaan (I) menjadi fungsi dari , yaitu: 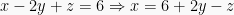. Kemudian subtitusikan pada persamaan (II) dan (III), menjadi

Persamaan (II):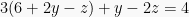 

Selesaikan, didapat: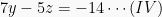 

Persamaan (III): 

Selesaikan, didapat: 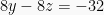 atau .

Persamaan (IV) dan (V) membentuk SPLDV

Dari persamaan (V), , kemudian disubtitusikan pada persamaan (IV), menjadi:

Kemudian subtitusikan 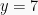 pada persamaan  diperoleh atau .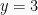

Subtitusik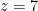an  dan  pada persamaan , menjadi 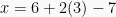, diperoleh .

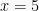Sehingga himpunan penyelesaian adalah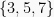 

2. Metode Eliminasi

Langkah penyelesaian pada metode eliminasi yaitu:

1. Eliminasi salah satu variabel sehingga diperoleh SPLDV
2. Selesaikan SPLDV yang diperoleh dengan langkah seperti pada penyelesaian SPLDV yang telah dibahas
3. Subtitusikan variabel yang telah diperoleh pada persamaan yang ada.

Sekarang coba kamu selesaikan contoh soal sistem persamaan linear tiga variabel di atas dengan menggunakan metode eliminasi!

Kontributor: Fikri Khoirur Rizal A.Q.
Alumni Teknik Elektro FT UI