Vi = Qx – Px
Vj = Qy – Py
Sehingga:
Vi = 5 – 2
Vj = 5 – 1
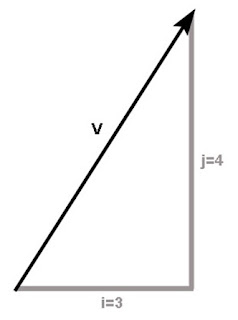
V = 3i + 4j
atau disingkat
V = (3, 4)
Vektor V hasil perhitungan di atas bukanlah suatu titik koordinat (3,4), hal ini harus dipahami supaya tidak terjadi kesalahpahaman. Untuk lebih jelas perhatikan contoh soal berikut:
Sebuah titik koordinat A(20,7) dipindahkan dengan menggunakan sebuah vektor V(10,–8), dimanakah posisi akhir titik A tersebut?
Jawab:
Posisi akhir dari titik A kita anggap titik B, sehingga:
Bx = Ax + Vi
By = Ay + Vj
Bx = 20 + 10
By = 7 + (– 8)
B = (30, –1)
Berdasarkan penjelasan dan contoh soal sebelumnya, maka terdapat perbedaan antara titik koordinat dan vektor.
Titik koordinat:
- Sebuah titik yang mempunyai lokasi
- Tidak mempunyai arah
- Tidak mempunyai nilai/besar/panjang tertentu
- Vektor tidak mempunyai lokasi
- Mempunyai arah atau dengan kata lain vektor adalah lintasan dari satu titik ke titik lain
- Mempunyai nilai/besar/panjang tertentu
Panjang Vektor
Untuk menghitung besar atau panjang vektor dapat digunakan teorema Phytagoras yang sudah kita kenal.
Contoh:
Sebuah vektor V(3,4), maka panjang vektor tersebut adalah:
│V│ = √(i² + j²)
│V│ = √(3² + 4²)
│V│ = √(9 + 16)
│V│ = 5
Skala Vektor
Panjang sebuah vektor dapat diatur sesuai dengan kebutuhan. Contoh sebuah vektor V(2,0) diperpanjang dua kali lipat, sehingga menghasilkan 2V(4,0).
Vektor V juga dapat diperkecil dengan skala=0.5, sehingga menjadi ½V(1,0).
Rumus untuk perkalian vektor dengan skala adalah:
SV = (Si + Sj)
dengan S adalah Skala.
Pada perkalian skala dengan vektor juga berlaku:
S│V│ = │SV│
Contoh:
Sebuah vektor V(3,4) dikalikan dengan skala=5, buktikan bahwa 5│V│ = │5V│.
Jawab:
│V│ = √(3² + 4²)
│V│ = 5
5V = (5×3 , 5×4)
5V = (15, 20)
│5V│ = √(15² + 20²)
│5V│ = 25
Sehingga:
5│V│ = │5V│
5×5 = 25
Dengan menggunakan skala, sebuah vektor dapat juga dibalik arahnya.
Contoh:
Sebuah vektor V(2,0) carilah invers vektor atau vektor yang berlawanan arah dengan vektor V(2,0).
Jawab:
Skala untuk membalik arah sebuah vektor adalah –1.
V(2,0) invers dari V adalah –V=(–2,0)
Perkalian Titik Vektor
Operasi perkalian titik dua vektor digunakan untuk mencari sudut antara dua vektor dan mencari proyeksi vektor(orthogonal).
Rumus perkalian titik dua vektor V dan W adalah:
V.W = (Vi.Wi + Vj.Wj)
Contoh:
Dua vektor V(1,2) dan W(5,3), carilah hasil perkalian titik(Dot Product) dari dua vektor tersebut.
Jawab:
V.W = ((1×5) + (2×3))
V.W = (5 + 6)
V.W = 11
Sudut Dua Vektor
Sudut dua vektor dapat dihitung dengan rumus:
V.W = │V││W│Cos Ө˚
Ө˚ adalah sudut terkecil yang dibentuk oleh dua vektor V dan W.
Contoh:
Dua buah vektor V(3,0) dan W(1,1), buktikan bahwa sudut yang dibentuk kedua vektor tersebut 45˚ dan bukan 315˚.
Jawab:
│V│ = √(3² + 0²)
│V│ = 3
│W│ = √(1² + 1²)
│W│ = √2
V.W = ((3×1) + (0×1))
V.W = 3
Cos Ө˚ = (V.W) / (│V││W│)
Cos Ө˚ = 3 / (3×√2)
Cos Ө˚ = 1/√2
Ө˚ = 45˚
Dengan gambar dan perhitungan di atas diketahui bahwa nilai Ө˚ adalah sudut terkecil yang dibentuk yaitu 45˚.
Proyeksi Vektor
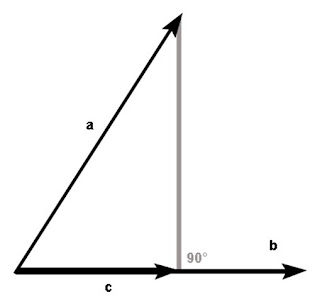
Dua buah vektor yaitu a dan b membentuk sebuah sudut, jika ditarik garis dari ujung vektor a ke vektor b secara tegak lurus, maka akan terbentuk sebuah vektor baru yaitu c yang searah dengan vektor b tetapi mempunyai skala yang berbeda. Vektor c inilah yang disebut dengan vektor hasil proyeksi vektor a ke vektor b.
Rumus untuk proyeksi vektor adalah:
c = [ (a.b) / │b│²] × b
atau
c = skala × b
dengan nilai skala = (a.b) / │b│²
Skala < 0 vektor berlawanan arah dengan vektor b.
Skala > 0 vektor searah dengan vektor b.
Skala = 0 sudut antara vektor a dan vektor b sebesar 90˚
Contoh:
Tentukan vektor hasil proyeksi dari vektor a(1,1) ke vektor b(8,0).
Jawab:
a.b = ((1×8) + (1×0))
a.b = 8
│b│ = √(8² + 0²)
│b│ = 8
│b│² = 64
c = [ 8 / 64 ] × (8,0)
c = [ 1 / 8 ] × (8,0)
c = (1,0)
Manfaat Vektor
Pada bagian ini ogut akan memberikan contoh-contoh manfaat vektor yang digunakan untuk pembuatan game 2D.
Contoh 1:
Tentukan titik berat(titik pusat) dari sebuah bujur sangkar yang keempat titik koordinatnya adalah A(2,2), B(4,2), C(4,4), dan D(2,4).
Jawab:
Pertama buat vektor V dari titik A ke C
Vi = Cx – Ax
Vj = Cy – Ay
Vi = 4 – 2
Vj = 4 – 2
V = (2,2)
Kalikan vektor V dengan skala=0.5
½V = ½(2,2)
½V = (1,1)
Tambahkan titik A dengan vektor ½V, sehingga titik berat dari bujursangkar tersebut adalah:
Ox = Ax + ½Vi
Oy = Ay + ½Vj
Ox = 2 + 1
Oy = 2 + 1
O = (3, 3)
Contoh perhitungan vektor di atas digunakan untuk memutar(rotasi) suatu objek pada pembuatan program di game 2D.
Contoh 2:
Sebuah bujursangkar mempunyai empat titik A(2,2), B(4,2), C(4,4), dan D(2,4). Buktikan bahwa titik O(3,3) berada di dalam bujursangkar, dan titik P(5,3) berada di luar bujursangkar.
Jawab:
Buat dua buah vektor V1(2,0) dan V2(0,2), buat juga vektor dari titik A ke titik O dan P, V3(1,1) dan V4(3,1).
Dengan menggunakan rumus proyeksi vektor dapat ditentukan apakah titik O dan P berada di dalam atau di luar bujur sangkar.
V5 = [ (V3 .V1) / │V1│² ] × V1
Skala1 = (V3 .V1) / │V1│²
V6 = [ (V3 .V2) / │V2│²] × V2
Skala2 = (V3 .V2) / │V2│²
Jika nilai 0 ≤ skala1 ≤ 1 dan 0 ≤ skala2 ≤ 1, maka dapat dipastikan titik O(3,3) berada di dalam bujursangkar.
Skala1 = ((1×2) + (1×0)) / (2² + 0²)
Skala1 = 2/4
Skala2 = ((1×0) + (1×2)) / (0² + 2²)
Skala2 = 2/4
Sekarang membuktikan titik P berada di luar bujursangkar:
Skala1 = (V4 .V1) / │V1│²
Skala2 = (V4 .V2) / │V2│²
Skala1 = ((3×2) + (1×0)) / (2² + 0²)
Skala1 = 6/4
Skala2 = ((3×0) + (1×2)) / (0² + 2²)
Skala2 = 2/4
Skala1 tidak memenuhi maka titik P berada di luar bujursangkar.
Kegunaan dari contoh soal No.2 di atas adalah dapat dipakai untuk mendeteksi tabrakan antara dua objek, seperti peluru menabrak pesawat dan pesawat menabrak musuhnya.
Update 28 Des 2015
Berikut ini adalah contoh program game yang menggunakan vektor untuk menyelesaikan perhitungan matematikanya.













0 comments:
Post a Comment